Проверка наличия седловой точки без расчёта частот

[Vit Nhoc]

Часто квантовики сталкиваются с дилеммой: считать молекулу хочется с симметрией, так быстрее, но нет уверенности, что будет найден минимум а не седловая точка. Обычно эту проблему решают, проводя после оптимизации расчёт частот. Но этот расчёт может быть относительно дорогостоящий, а иногда, полагаю, и просто почти невозможен, если метод не предлагает аналитических силовых постоянных (расскажите, как часто такое бывает).
Для решения этой проблемы, я полагаю, есть второе решение - немного исказить геометрию молекулы, понизив симметрию, и повторить оптимизацию. Если это был минимум - оптимизация в него же вернётся, а если седловая точка - уйдёт далеко. Chemcraft для этого предлагает добавить небольшие случайные числа к координатам атомов опцией Edit/Make small random displacements. В этой связи я вначале немного испугался, нет ли шанса шагнуть не туда и получить неправильный координат; речь о том, что не совсем понятно, как в седловой точке располагаются изолинии, если строить многомерный график по всем координатам. Чтобы с этим разобраться, я построил простой 3d график с двумя минимумами - гауссовыми пиками и визуализировал его в Chemcraft:



Как корректнее называть такой график - 2d graph или 3d graph?
Тут видно что изолинии могут пересекаться в седловой точке, т.е. встречаются две изолинии, и если шагнуть влево/вправо - энергия понизится, а если шагнуть вверх/вниз - энергия повысится. Но в любом случае, как я понял, последующая оптимизация приведёт не к этой седловой точке, а к одному из минимумов.
Я вот думаю: нельзя ли ещё усовершенствовать этот подход, чтобы тратить на него ещё меньше компьютерных ресурсов. Оптимизация в симметрии C1 занимает многовато времени, а теоретически можно сделать всего один single point, близкой точки, чтобы убедиться что энергия упадёт и значит это была седловая точка (на моём графике - вправо или влево). Возможно, идея пока слишком нечёткая/интиутивная.

[Гесс]

Ох... Слона будем есть по кусочкам...

но нет уверенности, что будет найден минимум а не седловая точка. Обычно эту проблему решают, проводя после оптимизации расчёт частот.

Вообще говоря подтверждение того что оптимизация пришла в минимум путем расчета частот - это правило хорошего тона независимо от использования симметрии.

Но этот расчёт может быть относительно дорогостоящий, а иногда, полагаю, и просто почти невозможен, если метод не предлагает аналитических силовых постоянных (расскажите, как часто такое бывает).

Тут много всего и сразу.
Да, расчет частот это недешево. Поэтому применяют разные извращения. (см в конце этого параграфа).
Если нет аналитических вторых производных - считают численно. Это 6*N+1 синглпоинт где N это число атомов молекуле, для случая несимметричных молекул. В случае симметричных молекул (если код это умеет) число синглпоинтов сократится. Численные частоты доступны в любых методах. Аналитические частоты в большинстве популярных пакетов доступны на любом ДФТ (иногда недоступны для meta-GGA, но скажем на чистом GGA {например PBE} доступны практически везде). Для дорогих методов типа каплдкластера аналитические производные доступны редко (у CFOUR есть почти всё, но CFOUR это CFOUR https://cfour.uni-mainz.de/cfour/index. ... requencies).
Рекомендую посмотреть напрмер о dertype в PSI4 https://psicode.org/psi4manual/master/freq.html
Для пакетов с Periodic Boundary Conditions (твердотельное ДФТ) численный расчет частот является основным или единственным вариантом.
Традиционная удешевлялка расчета частот - это их расчет в том же методе но с несколько сокращенным базисом. Является на самом деле весьма грубым хаком, так как ППЭ с разными базисами может и не совпадать, но обычно работает хорошо. Классический метод тех времен когда компьютеры были большими а системы маленькими. Сейчас применяется реже.
В Орке есть PartialHess, но его основное предназначение не удешевление расчета, а неучет частот для определенного фрагмента системы (катализаторщики весьма благодарны, ввиду фишечек термохимии).

есть второе решение - немного исказить геометрию молекулы, понизив симметрию, и повторить оптимизацию. Если это был минимум - оптимизация в него же вернётся, а если седловая точка - уйдёт далеко.

Может поможет, а может и не поможет. Если случайный сдвиг (в многомерном пространстве!) дал геометрию из которой градиент оптимизации будет направлен НЕ к исходной геометрии - да, оптимизация пройдет мимо исходного седла и возможно уйдет к минимуму. А если исходный сдвиг (а он ОЧЕНЬ вероятно выше по энергии чем исходное седло, так как всего частот у молекулы 3N-6, а понижающих в классическом седле всего одна), будет иметь градиент обратно к исходной геометрии - то в нее он и придет.
Плюс еще всякие артефакты ППЭ. Скажем оптимизируйте ацетон на B3LYP/aug-cc-pVTZ на дефолтных настройках сетки и попробуйте там найти геометрию без мнимых частот (кстати в случае бутанона на этом функционал-базисе в турбомоле не помогает даже улучшение сетки по максимуму). Так что наличие отрицательных частот тоже не всегда однозначный ответ.

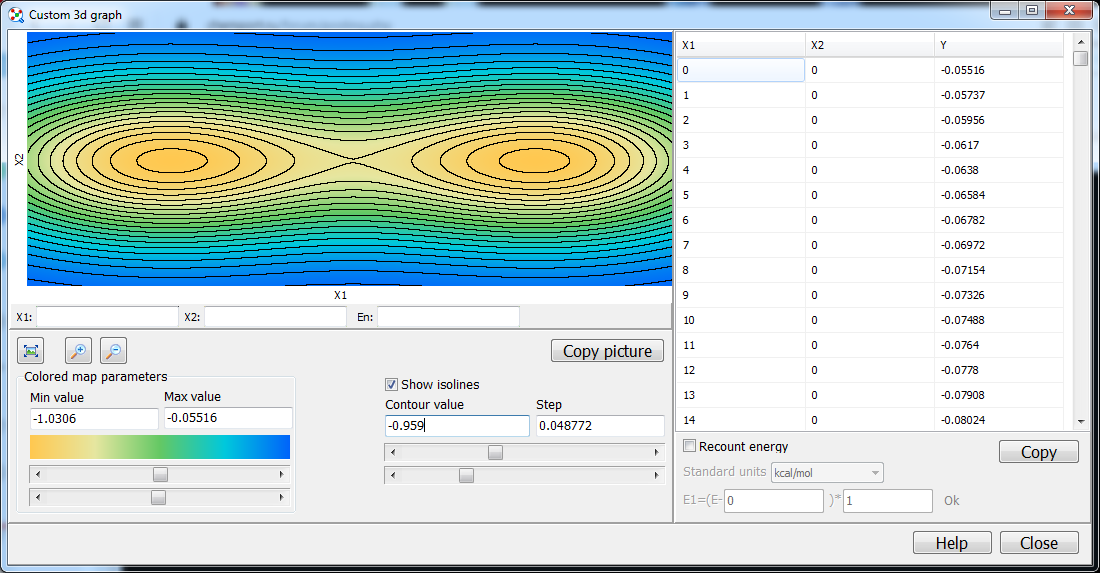
речь о том, что не совсем понятно, как в седловой точке располагаются изолинии, если строить многомерный график по всем координатам.

При размерности выше 2 - изоповерхности. - сдвиг по любому направлению кроме одного (в многомерном прострастве) ведет к пересечению изоповерхностей более высокой энергии, сдвиг по одному и лишь одному направлению ведет к пересечению изоповерхностей более низких энергий. К сожалению представить это в пространстве больше 3 - достаточно затруднительно, а визуализировать даже ситуацию с 3 геометрическими размерностями и 4ой энергией, на двухмерном рисунке очень проблематично. Можете попробовать представить sci-fiction movie в котором космический челнок вплывает в ангар станции, при этом его движение направляется силовыми щитами от стен (силовые щиты по голливудской классике стеклопрозрачные). При этом движение челнока вверх-вниз равно как и вправо-влево будет встречать сопротивление щитов, тем большее чем ближе к стенам он приблизится. Движение же вперед-назад в данном случае "изоэнергетично", но если мы представим что на челнок действует "затягивающее" поле от "концевой" стены ангара ну и чтоб не мелочиться "затягивающий луч" от корабля противника (который пытается вытянуть челнок обратно в открытый космос), то вы получите 3-мерную ППЭ с четвертым параметром энергии. Фух, бобер выдохнул...
2D graph как у вас - такое часто строят для обьяснения концепций, например загуглите картинки для Nudged elastic band и реже для практического применения. Тут важно из всего многообразия координат (в том числе и в превую очередь внутренних), выбрать 2 существенные. Для переноса протона это могут быть расстояния от него до двух атомов между которыми он мигрирует (https://www.researchgate.net/publicatio ... gures?lo=1 рисунок 5) для синхронных процессов - некие ключевые расстояния на разных концах молекулы. (https://www.researchgate.net/publicatio ... gures?lo=1 рисунок 2). Это могут быть углы и даже диэдралы или Linear Combination of Coordinates
Кроме того построение подобных графиков это ОЧЕНЬ дорого, потому как каждая точка на графике это отдельная ОПТИМИЗАЦИЯ с 2 зафиксированными параметрами. И их нужно ну как минимум сотня, чтобы график выглядел хоть как то (10x10).

а теоретически можно сделать всего один single point, близкой точки, чтобы убедиться что энергия упадёт и значит это была седловая точка (на моём графике - вправо или влево).

См. выше - при рандомном сдвиге из седла в произвольном направлении в многомерном пространстве ваша энергия практически наверняка возрастет. Она упадет лишь если вы сдвинетесь вдоль (или почти вдоль) "пути минимальной энергии", который часто называют IRC тупо изза алгоритма который по этому пути двигается. Но чтобы знать это направление - вам нужен или расчет частот, или построение несколько-мерного ППЭ (что намного дороже). Не, можно конечно накидывать рандомно сотни синглпоинтов и в зависисмости от размера системы и формы ППЭ, рано или поздно (если вы стартуете из седла) вы поймаете точку более низкую по энергии. Только учтите что 6*N синглпоинтов в чиленных частотах дадут ответ точно, а рандомные сдвиги - это лотерея. Можете поймать более низкую энергию с первого выстрела. А можете не поймать ничего и из 100*N попыток.

[Гесс]

Несколько оффтоп - если оптимизация в C1 вашей системы слишком долго/дорого - я бы рекомендовал либо понизить базис, либо удешевить метод, либо упростить систему. Я могу попробовать дать какую то рекомендацию из своего опыта если вы покажете о чем речь.
Ну и ответ пригодный абсолютно всегда (и столь же бесполезный) - нужен компуктер побольше.

[Vit Nhoc]

См. выше - при рандомном сдвиге из седла в произвольном направлении в многомерном пространстве ваша энергия практически наверняка возрастет. Она упадет лишь если вы сдвинетесь вдоль (или почти вдоль) "пути минимальной энергии", который часто называют IRC тупо изза алгоритма который по этому пути двигается. Но чтобы знать это направление - вам нужен или расчет частот, или построение несколько-мерного ППЭ (что намного дороже).

Так возрастёт-то она возрастёт, но это не значит, что оптимизация возвратится к этой же седловой точке. Либо я туплю, либо вы, сорри. Посмотрите ещё раз на рисунок выше - если сделать шаг чуть вверх, то энергия возрастёт, но оптимизация пойдёт в направлении вниз и либо направо либо налево (перпендикулярно изолинии), т.е. к настоящему минимуму, а не к седлу. Если вы говорите, что оптимизация в C1 может привести к седловой точке, я это совершенно не понимаю. Не знаю каким примером описать, ну вот - если вы положите шарик верблюду на горб, он стопроцентно куда-то скатится. Другое дело, что оптимизация в C1 может дать отрицательные частоты из-за численного шума. Но это не будет седловая точка.

[Гесс]

Оптимизация в любой симметрии, включая С1 как ее отсутствие, может легко заканчиваться в седловых точках. А в грустных случаях и в точках с бОльшим количеством мнимых частот.
Как раз сдвиг строго вверх или строго вниз на вашей картинке приведет к геометрии где градиент будет направлен строго обратно в седло.
Сдвиг "не строго вверх" имеет некоторые шансы скатиться в минимум, это зависит в том числе от того насколько велик сдвиг. Если вы слишком близко к критической точке, выше ее и не делаете гессиан - есть очень хорошая вероятность скатиться обратно в критическую точку независимо от ее NImag. Да, это неинтуитивно, но часто именно так.
В качестве примера - возьмите staggered ferrocene (он D5d), сделайте ему оптимизацию и частоты, увидите что он переходное состояние (это отлично укладывается в то что вы говорите). После этого попробуйте малый дисплейсмент и посмотрим - сможет ли он уйти в eclipsed минимум. Если вдруг справится - следующий шаг, берем эту геометрию (она уже формально С1 хотя и выглядит как D5h), и считаем катион радикал, оптимизация и частоты.
Я со своей стороны прилагаю две описанные выше минимизации - нейтрал на PBE/def2-TZVP, катионрадикал на PBE/ma-def2-TZVP (но сомневаюсь что с другими базисами вы придете к чему то иному). Нейтральный ферроцен был оркой опознан как Ci, катионрадикал чистой воды C1. Численный шум - это от силы пара десятков обратных сантиметров. У катионрадикала - 150плюс.
Пример взят ввиду доступности - первый расчет занимает 4 минуты на 12 ядрах, второй - 11 минут на 36 ядрах, ну то есть на 4 ядрах я думаю не многим больше (а может даже меньше) часа.

[Vit Nhoc]

Да, действительно. Для меня это странно, до сих пор не понимаю как такое получается. Хотя у первого вашего файла есть симметрия Ci.
Вот ещё одна мысль. Как часто расчёт частот численно даёт неправильные результаты из-за неучёта криволинейности или численных ошибок? Я имею в виду, что надо чуть-чуть сдвинуть молекулярную геометрию и посмотреть как меняется энергия; если вы меняете её очень мало, то будет ошибка из-за того что сходимость SCF не аналитический процесс и даёт ошибку, а чем меньше шаг тем меньше разница энергий; если шаг слишком большой, то будет ошибка из-за ангармоничности. И эту ошибку можно уменьшить, если сдвигать не декартовы координаты, а естественные, описываемые расстояниями и углами. Например, у вас молекула воды: если вы сдвигаете атом водорода в декартовых координатах и на большое значение, то поменяется длина связи O-H, поэтому лучше описать эту молекулу не декартовыми координатами, а двумя расстояниями O-H и углом H-O-H. Тогда при шаге по углу длины связей O-H не поменяются, поэтому подход будет более надёжный. Я вижу реализацию этого в Chemcraft так: пользователь задаёт, какими естественными координатами описывается его молекула, Chemcraft генерирует множество структур, в которых по этим координатам делались шаги, далее пользователь считает эти структуры, и далее они все снова загружаются в Chemcraft и программа считает силовые постоянные, а по ним частоты и всё прочее.

[Гесс]

Хотя у первого вашего файла есть симметрия Ci.

Есть. Она самопонизилась до туда из D5d (я кинул в расчет геометрию которая в стандартах Кемкрафта и не задавал сам никакой симметрии) хотя и не обязана была этого делать. Это то что у меня было под рукой. Я не делал отдельного расчета с дисплейсментами. Я прям сильно предполагаю что после небольшого дисплейсмента (который сделает молекулу формально C1, но все еще вблизи этой критической точки) мы придем в тот же самый TS с теми же самыми частотами только формальная симметрия будет ниже).

В следующем тексте я потерялся и запутался. Там слишком много всего и одновременно. Скажем при чем там ангармоничность я вообще не понял.
Вы говорите про расчет в internal coordinates вместо cartesian coordinates. Так это дефолт для большинства молекулярных кодов. То есть и орку и гауссиан можно заставить оптимизировать в декартовых координатах, но это дополнительные ключи в теге Opt.
Свой набор внутренних координат орка прописывает в блоке "INTERNAL COORDINATES" в самом начале и в начале каждого шага оптимизации.
Кодов которые не умеют во внутренние координаты среди непериодического софта не так много.

Я вижу реализацию этого в Chemcraft так: пользователь задаёт, какими естественными координатами описывается его молекула, Chemcraft генерирует множество структур, в которых по этим координатам делались шаги, далее пользователь считает эти структуры, и далее они все снова загружаются в Chemcraft и программа считает силовые постоянные, а по ним частоты и всё прочее.

Кажется вы хотите из Кемкрафта сделать внешний интерфейс к какому то компьютерному коду который будет нарезать для квантохимического кода (далее КХК) задачу (в данном случае набор синглпоинтов) и пост-обрабатывать результаты.
Очень аналогичную задачу решает ASE на который я ссылался в соседней теме https://wiki.fysik.dtu.dk/ase/about.html
Например в приложении к оптимизации в VASP (который во внутренние координаты не умеет) - ASE создает внутренние координаты, посылает задачу в васп, получает от Васпа обратно энергию и градиенты, на их основе и с учетом заданных во внутренних координатах ограничениях создает новую геометрию, которую перегоняет в декарты, отправляет васпу, и т.д. В случае расчета частот ASE нарезает набор синглпоинтов, скармливает их васпу, собирает аутпуты, на их основе считает частоты и прочую термохимию. (Я этим не пользуюсь тупо потому что ВАСП и сам может посчитать частоты без помощи ASE, а нафига мне подобные прокладки с путанным синтаксисом).
Впринципе интерфейсенье чем то какого то КХК - это не настолько редкое решение. Ну скажем ADCC https://adc-connect.org/v0.15.7/calculations.html весьма "несамостоятельный" код, он первым делом посылает scf-задачу в pyscf или PSI4, получает оттуда сведенный scf на котором начинает строить свою черную магию (расчет УФ спетра методом algebraic-diagrammatic construction).
Вопрос в следующем: что в вашем алгоритме нарезки задачи (в частности создания новых координат для численного расчета частот) лучше чем в дефолтных алгоритмах софта.
Если вы смотрите в сторону кодов которые не умеют использовать внутренние координаты - то я не вижу смысла вам конкурировать со все тем же ASE. ASE это абсолютно уродливый визуализатор (ну точнее у него есть gui и этот gui страшен как Нургл), у ASE предельно неудобный построитель. о есть в тех аспектах где Кемкрафт обьективно лучший - ase весьма посредственен в лучшем случае. С другой стороны это питоновский код прекрасно исполняемый напрямую на серверах (а в случае кемкрафта я так понимаю придется скачивать десятки аутпутов с сервера чтобы обрабатывать их локально), отлично работающий с периодикой (построить кристалл fcc меди с данным шагом решетки, сделать 111 поверхность с толщиной в 4 слоя, добавить 15 ангстремов вакуума, заморозить нижние слои, сохранить в POSCAR формат - это меньше десяти строк, включая подтягивание необходимых библиотек. Еще десяток строк на задание деталей расчета, и несколько строк собственно на сабмит расчета.
Это реально интерфейсер, в отличие от прочих gui (как TMoleX и GausView), которые помогут создать инпут и возможно даже запустят его, но не будут заниматься постобработкой результатов.

[Vit Nhoc]

Гесс
Я посмотрел один расчёт Gaussian, выбрал в Chemcraft Tools(слева)/Show internal parameters used in optimization, и с небольшим удивлением убедился, что Gaussian умеет замыкать циклы, т.е. в список внутренних параметров входят все длины связей в цикле. Если строить обычную z-матрицу, нельзя замкнуть цикл. Значит Gaussian использует какой-то изощрённый алгоритм построения декартовых координат по набору внутренних параметров, может быть итерационный?
Вроде как с таким списком внутренних параметров мне придраться не к чему, т.е. их корректно назвать также естественными координатами (в них входят все связи). И значит вы хотите сказать, что когда Gaussian считает частоты численно, или считает ангармоничные частоты, он шагает именно по этим внутренним параметрам? Я полагаю, это должно означать именно итерационный алгоритм пересчёта внутренних координат в декартовы.

[Гесс]

1) Гауссиан считает (по умолчанию) в redundant internal coordinates
Смотреть https://www.cup.uni-muenchen.de/ch/comp ... ndant.html или в https://gaussian.com/opt/

Like the default algorithm for minimizations, it performs optimizations by default in redundant internal coordinates.

Redundant означает избыточный, и таки да, там больше чем минимальный набор координат которым например является Z-matrix.
redundant internal coordinates насколько мне известно является всреднем по больнице самым быстрым для сведения и стандартом/дефолтом в большинстве пакетов поддерживающем эту фишку (Гауссиан, Орка, Турбомоль и пр, в то же время CFOUR работает в Z-matrix).
Иногда это порождает в людях убежденность что оптимизация в декартовых координатах НАМНОГО медленнее. Это не так. Мы когда то делали оценку, получается что redundant internal coordinates быстрее процентов на 20, зато в декартах нельзя влететь в некоторые проблемы внутренних координат.
2) Проблемы внутренних координат.

т.е. в список внутренних параметров входят все длины связей в цикле

Если мы говорим про расстояния - да, туда входят все "короткие"/"связевые" расстояния, и в случае "несвязанных" комплексов еще и как минимум одно расстояние между "несвязанными" кусками. Первой проблемой для внутренних координат будут большие подковообразные молекулы - хвосты не имеют координаты которая бы предотвращала их "склещивание" https://www.chemport.ru/forum/viewtopic ... 2&p=845610 Такую внутреннюю координату можно добавить вручную (в Гауссиане это AddRedundant который на самом деле работает как ModRedundant), но это ж думать надо между чем и чем какую координату... А оптимизация в декартовых координатах от этого свободна.
Вторая проблема внутренних координат это диэдралы в состав которых входят 3 атома (из 4) угол между которыми в ходе оптимизации становится 180 градусов. Разумеется в этом случае смысл диэдрала теряется и наш любимый Гауссиан склеивает лапки (текст ошибки не вспомню, но там напрямую указывается список атомов попавших в переплёт. Алгоритм строит набор координат так чтобы углов около 180 небыло, но пути оптимизации неисповедимы. Набор внутренних координат не меняется в ходе расчета (после их инициации в самом начале).
3) Это построение неитеративно, как минимум для ковалентно-связанных (одномолекулярных) систем точно, для комплексов - наверняка. Все длины связей которые под дефолтом (он на основе атомных радиусов) попадают в список сразу, если у атома есть N связей, то между каждой парой связей будет инициирован угол. По диэдралам не помню. Какой алгоритм для задания межмолекулярных не знаю, но там внутренние координаты всеравно хуже чем декарты (если мы говорим про плоские ППЭ слабосвящанных комплексов, если у вас катион калия сольватированный 4 молекулами воды которые изначально ориентированы на калий кислородами - внутренние координаты справятся отлично, а вот кластер из 5 молекул метана можно возить до бесконечности).

[Гесс]

алгоритм построения декартовых координат по набору внутренних параметров

строго наоборот - в инпуте у него декарты, на их основе он строит внутренние координаты.

Чуть больше теории про то как они строятся, как используются и где у них затык в больших матрицах - рекомендую блок "Redundant Internal Coordinates" в маунале орки (2 страницы прилагаю)

Orca Redundant Internal Coordintaes.pdf

И значит вы хотите сказать, что когда Gaussian считает частоты численно, или считает ангармоничные частоты, он шагает именно по этим внутренним параметрам?

Я этого в такой формулировке не утверждал. Они точно задействованы в оптимизации, но если бы численные частоты делались из этих координат по принципу "шаг влево - шаг вправо", то мы бы получили ОЧЕНЬ избыточное ППЭ. Точный алгоритм я по быстрому не нагуглил, https://zenodo.org/record/44767#.Y_0bii8w3bc пишет что там просто поочередное смещение по декартам атома за атомом (это явно простейшее решение). Ангармонизм там скорее всего просто построением дополнительных смещений. Впрочем я не лезу в "ангармонические частоты" таким манером, а тот ангармонизм который пилят в нашей группе построен вообще на других принципах. Так что тут врать не буду.
Вон статья https://pubs.acs.org/doi/10.1021/jp3127576 (pdf прилагаю) предлагает метод расчета частот именно на основе внутренних координат (там явно надо менять одновременно по несколько координат), и они даже показывают что можно делать быстрее чем в декартах, но если я правильно трактую последнюю диаграмму - для молекулы C₂₀H₄₀OH выиграш составит всего 5% и явно будет снижаться дальше. Напрашивается ответ что для больших систем это просто бесполезно. На малых да, можно играть. Они сделали ставку на малые молекулы и высокие уровни теории и типа CCSD. Да, тут оправданно, но насколько востребованы такие расчеты?

jp3127576.pdf

P.S. Ну и вот еще (не)легкого чтива про внутренние координаты, как и строить, как использовать в частотах, как перегонять в декарты.

180.pdf

Это Шлегель, его именем один из алгоритмов построениея Гессиана в Орке назван

The different guess Hessians can be set via the InHess option which can be either unit, Almloef, Lindh, Swart or Schlegel in redundant internal coordinates. Since version 2.5.30, these model force-fields (built up in internal coordinates) can also be used in optimizations in Cartesian coordinates.

[amge]

Часто квантовики сталкиваются с дилеммой: считать молекулу хочется с симметрией, так быстрее, но нет уверенности, что будет найден минимум а не седловая точка.

Более того, часто оптимизация симметричного начального приближения, даже с заданной явно С1, сходится, не нарушая симметрию, причем получившаяся структура может быть не только седлом, но и вообще нестационарной точкой.

Обычно эту проблему решают, проводя после оптимизации расчёт частот. Но этот расчёт может быть относительно дорогостоящий...
Для решения этой проблемы, я полагаю, есть второе решение - немного исказить геометрию молекулы, понизив симметрию, и повторить оптимизацию.

Как правильно заметил Гесс, нет никакой гарантии, что случайно искаженная геометрия не вернется обратно. Более правильно все же посчитать гессиан и приложить его к инпуту оптимизации. К сожалению, орке это не помогает. Тогда вручную исказить геометрию, но не случайно, а по мнимой моде.
Если гессиан считать долго, то, пользуясь тем, что геометрия обычно слабо зависит от метода, можно посчитать его каким-нибудь быстрым (но достаточно адекватным) методом. Я, например, постоянно этим пользуюсь, подкладывая орке природовские гессианы для оптимизации переходных состояний.

[amge]

Иногда это порождает в людях убежденность что оптимизация в декартовых координатах НАМНОГО медленнее. Это не так. Мы когда то делали оценку, получается что redundant internal coordinates быстрее процентов на 20, зато в декартах нельзя влететь в некоторые проблемы внутренних координат.

Поддерживаю! Я бы сказал, скорее на 50%, но в любом случае не слишком критично. Зато, действительно, никаких проблем. А в особых случаях, например, для ковалентно несвязанных комплексов, и быстрее.

[Vit Nhoc]

Первой проблемой для внутренних координат будут большие подковообразные молекулы - хвосты не имеют координаты которая бы предотвращала их "склещивание"

Там в вашей теме не хватает картинки, а я подумал что мне надо сделать опцию Tools[слева]/Show internal parameters used in optimization для Орки (сейчас есть для Гауссиана):

изображение_2023-02-28_112613391.png

[Vit Nhoc]

Сделал Show internal parameters used in optimization для Орки, и всплыло два момента. Во-первых, я не понимаю что такое параметр L, например строчка

161. L(O 28,H 33,O 31,H 41, 2) 176.1063 0.202945

В секции Redundant Internal Coordinates.
И создалось ощущение, что Орка намного хуже чем Гауссиан выбирает эти координаты правильно, вот моя молекула:

internparamsorca.png

[Гесс]

Ну систему которую я считал 8 лет назад в другом институте имея другой ноут я уже не найду (оно не было опубликовано), по памяти это чтото типа вот этого (построил по быстрому в Chemcraft).

Smthlike.jpg

В TIPS-pentacene-овой части я уверен, линкер там вполне возможно другой (возможно бутан или пентан). Но если между TIPSами не будет построено дополнительного Redundant coordinat (или шаг оптимизации не будет загнан в минимум) то с очень хорошей вероятностью эта система помрет на первых 10 шагах оптимизации.
Геометрию прилагаю если захотите тестить.

C62H46.xyz

[Гесс]

Сделал Show internal parameters used in optimization для Орки, и всплыло два момента. Во-первых, я не понимаю что такое параметр L, например строчка

161. L(O 28,H 33,O 31,H 41, 2) 176.1063 0.202945

В секции Redundant Internal Coordinates.

Дайте пожалуйста аутпут.

[Vit Nhoc]

Дайте пожалуйста аутпут.

Прикрепляю. Только версия Chemcraft, которая у вас, ещё не умеет читать секцию Redundant Internal Coordinates
в этом файле. Могу закачать версию которая умеет, если надо. Там например строка 393 - связь между совсем далёкими атомами.

[Гесс]

А, я уже посмотрел в своих аутпутах.
Насколько я могу судить это возникает когда первые три атома этого диэдральника близки к 180 (проблема о которой я писал выше) и орка создает две внутренние координаты, рискну утверждать что это проекция "почти развернутого" угла на плоскость которая включает в себя 4ый атом диэдральника. Я не уверен как именно эта пара внутренних координат должна решать проблему развернутого угла, но видимо как то решает, в отличие от Гауссиана падений Орки от этой ошибки я еще не видел.

[Гесс]

Там например строка 393 - связь между совсем далёкими атомами.

Про какую строку речь?

[Vit Nhoc]

Там например строка 393 - связь между совсем далёкими атомами.

Про какую строку речь?

В файле carb.out, в строке 322 начинается таблица Redundant Internal Coordinates, и в строке 393 параметр N66, явно нефизичный.